Per calcolare l’area della sezione maestra  ma anche delle altre sezioni nonché delle linee d’acqua e di qualsiasi forma geometrica irregolare ci sono 3 modi fondamentali:

• Disegnare la carena al computer con un programma cad specifico per il disegno ed il calcolo.
• Disegnare la sezione (o comunque una figura geometrica irregolare) in scala e misurarla con il planimetro. Il planimetro è uno strumento abbastanza preciso ma di costo notevole. Nel disegno tradizionale di una barca viene usato spesso per i calcoli preliminari.
• Calcolarsela  “a mano”.

Dei tre sistemi il primo è il più rapido. Bisogna comunque possedere un computer, un programma specifico e saperlo usare.
Il planimetro, se lo strumento è buono ed è usato bene, dà risposte rapide e abbastanza precise. Il planimetro costa  diversi soldi ed è uno strumento delicato, si usa solo per quella funzione ed è un’acquisto conveniente solo se si usa spesso.
Il metodo di calcolarsela “a mano” è di gran lunga il più complicato, può dare risultati sbagliati se usato male ma sfrutta il cervello che di solito è già in dotazione con il resto del corpo e quindi pagato (tanto vale usarlo il più possibile).
Vale pertanto la pena di perdere un pò di tempo per capire come si fa. Una volta capito il metodo si può scegliere di continuare a usarlo o passare al computer.

Cominciamo col dire che il caso che ci si presenta è quello di calcolare una superficie geometrica irregolare. Se la superfice è regolare ad esempio un triangolo allora si fa base x altezza e si divide per due e finisce lì.
Una superficie più complessa implica calcoli più complessi. Bisogna dire però che nel nostro caso ovvero quello di calcolare superfici inerenti la carena di una imbarcazione queste  sono simmetriche e tagliate da piani paralleli tra loro (linee d’acqua). Questa simmetria favorisce il calcolo.

Il calcolo dell’area evidenziata in giallo si può fare eseguendo un’operazione di integrazione, ovvero sommare tra loro tante aree elementari. L’operazione darà un risultato tanto più preciso quanto più piccole saranno le aree prese in esame.

I metodi principali di integrazione sono due : quello dei trapezi o di Bezout e quello di Simpson, vediamoli:
Metodo dei Trapezi o di Bezout
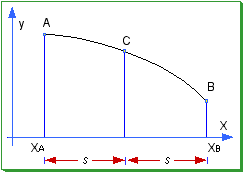
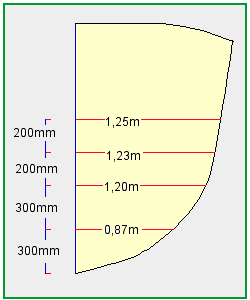
Dobbiamo calcolare l’area compresa dalla linea AB. Il metodo consiste nell’approssimare la curva AB con la spezzata ACDEFB e quindi calcolare l’area compresa da AB come la somma dei trapezi 1,2,3,4 e 5.

L’area del trapezio è data dal prodotto tra l’altezza e la semisomma delle basi e quindi :

Se la suddivisione del segmento xa-xb  viene fatta con intervalli tutti della stessa lunghezza s

allora la formula dell’ area totale diventa:

Concludendo possiamo dire che il metodo dei trapezi consiste nel suddividere la base della figura in un numero  n di intervalli tutti della stessa lunghezza, individuare le altezze originate da questa divisione e sommare tra loro la metà della prima, la metà dell’ultima e tutte le intermedie e moltiplicare questa somma per l’intervallo s.
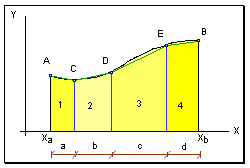
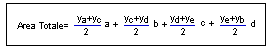
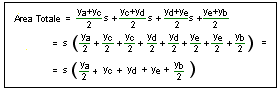
La forma generica della formula è quindi:

Il metodo dei trapezi è molto rapido e comporta calcoli abbastanza semplici. Difetta però di precisione come evidenziato nella figura seguente nella quale sono stati enfatizzate le porzioni di superfice calcolate in meno e quella in più.  Con un pò di pratica si può ottenere dati abbastanza precisi e comunque di precisione sufficiente nel calcolo preliminare.

Ricordiamoci sempre che se stiamo prendendo in esame la metà di una superficie simmetrica, il valore finale di A va raddoppiato. Può sembrare una notazione studipa ma, credetemi, capita di dimenticarsene o peggio di incorrere nell’errore di raddoppiarla successivamente, magari in fase di calcolo di volumi, ottenendo risultati “sballati”.

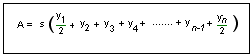
Regola di Simpson
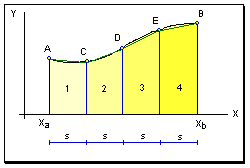
Anche qui si tratta di approssimare la superficie totale per somma di superfici elementari ma a differenza del metodo di Bezont non si prende in esame una linea spezzata per costruire dei trapezi ma una serie di linee curve (parabole).
Le regole di Simpson sono due:

• la prima, detta delle 3 ordinate,  si applica a figure suddivise in un numero dispari di ordinate.
• la seconda, detta delle quattro ordinate, si applica quando le ordinate sono un multiplo di 3 più 1 ovvero 4, 7, 10, 13, 16 ecc.

Vediamo la prima regola:

la formula  è la seguente :

e, come abbiamo detto si applica per un numero dispari di ordinate. Vediamo quindi un caso con più di 3 ordinate:

applicando la formula della prima regola  abbiamo:

Invece con la seconda regola di Simpson possiamo calcolare l’area di superfici divise per un numero di ordinate multiplo di 3 più uno e quindi 4, 7, 10, 13, 16 ecc
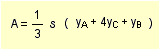
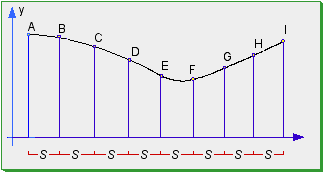
la formula si esprime così:

e, ad esempio :

applicando la formula della seconda regola avremo:

---

Queste sono le formule del metodo di Simpson. Passiamo a vedere in pratica il calcolo di una sezione così come era richiesto:

mettiamo in ordine i valori inuna tabella e otteniamo:

Per ottenere l’area totale sommiamo le due semiaree e moltiplichiamo per due (stiamo calcolando la metà della sezione)
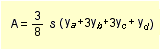
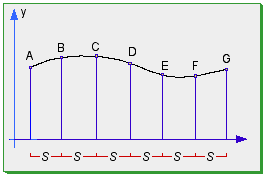
Ci sono altri metodi  più elaborati che non riporto anche perchè non li conosco e non li ho mai usati.

Questi calcoli non sono complicati e hanno il vantaggio di essere rapidi. Se uno si fa il suo bel disegnigno col computer ed un programma adatto allora il programma, finito il disegno, gli dice  aree, volumi, distribuzione dei volumi, pesi e magari anche la velocità prevista. Se poi il disegno è fatto bene allora si possono passare i dati direttamente ad una macchina di taglio che provvede a produrre ordinate in CM o acciaio in un attimo. Non è fantascienza ma è come effettivamente si lavora su scala industiale. Per noi semplici autocostruttori, che ci sforziamo di pensare alla nostra barchetta anche quando tutto intorno a noi gira vorticosamente, forse è meglio fare due conti “a mano” che ci apre la mente e ci tiene svegli.
Spero di essere stato chiaro e non aver commesso errori nella spiegazione. Ringrazio in anticipo chi rilevasse errori e/o inesattezze  pregandolo di comunicarmelo in modo che possa corregermi.

---

Bibliografia
– Fondamenti di idronautica di U.F.Costaguta – Hoepli – Milano 1981
– C.so di progettazione As.Pro.Na.Di – Statica dei Galleggianti